为何赌徒心态终究输光 非遍历性系统中的生存法则
作者:雪鹅,来源:公众号DataCafe
想象你带着1000元起始资金参加这样一个翻硬币挑战游戏,你可以选择一直玩下去:
每轮抛一次硬币,
抛到正面,财富增加 80%。
抛到反面,财富减少 50%。
听上去是个稳赚不赔的游戏!
但现实是……
如果让10万个玩家参加这个游戏,并让他们各自玩100轮,你会发现:他们的平均财富确实在指数增长,但绝大多数人最后的财富竟然不到72元,甚至破产!
为什么平均财富是增长的,但大多数人却越玩越穷?
这就是典型的非遍历性陷阱。总觉得再来一局就能翻盘,恰恰是因为我们误把群体平均当成了个体命运。

非遍历性的陷阱:长期平均≠ 你的真实命运
什么是遍历性?
遍历性(Ergodicity)这个概念最早出现在统计物理学中,也在概率论、金融、行为科学、机器学习等领域产生深远的影响。它试图回答的核心问题是:长期平均值,是否适用于个体?我们在做决策时,到底该相信‘长期平均’,还是‘一次次亲身经历’的现实?
19世纪,物理学家路德维希·玻尔兹曼(Ludwig Boltzmann)研究气体分子运动时提出了遍历性假设:如果观察一个气体分子足够久,它会遍历所有可能的状态。
想象一个封闭的气体容器,容器中有无数气体分子,每个分子都在碰撞过程中经历不同的速度轨迹。单个分子的长期轨迹和整个气体的统计分布是相同的,这意味着我们可以用某个时刻所有分子的状态,来推测单个分子的长期轨迹。
这就是著名的玻尔兹曼的遍历性假设。

数学上,遍历性意味着:
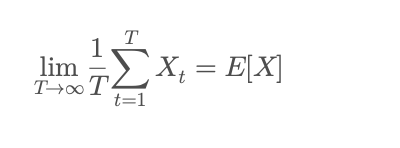
左侧是时间平均:描述一个个体在足够长的时间里,多次经历同一过程后所得的平均结果;
右侧是群体平均:描述在某一时刻观察无数个体的结果所得的统计期望。也就是说:当系统满足遍历性条件时,单个个体的表现最终会收敛到群体的“长期平均”。
如果世界是遍历的,每个人的财富最终都会趋近于社会的平均财富水平。在遍历的世界,所有人都能体验到所有可能的经济状态(富有、贫穷、成功、失败),个体的命运总会收敛到群体的“长期平均”。
但现实生活往往是非遍历的:个体的资源有限,往往在经历到所有可能的路径前就因某次失败直接出局。
我们经常听到这样一些具有引导性的言论:
“某行业的平均年收入过百万。”
“某人30岁就财务自由,创业只花了两年。”
“某指数基金长期年化收益高,只要坚持投就会变富。”
……
这些看似合理的统计数据仿佛在告诉我们一个确定的真相。好像只要行动,长期平均收益就会适用于个体。但这些个案属于路径依赖+不可复制的非遍历过程。模仿者无法经历相同历史背景、关系网络、运气节点,甚至不知道隐藏失败者的数量。
数据告诉你群体长期的平均值,但现实却充满短期的“断崖式失败”。
这正是非遍历性最隐蔽的陷阱 —— 大数据统计的平均值 ≠ 个体的真实命运。
一次崩溃对于个体来说可能再也无法弥补,一次失败可能让人彻底出局,无法再回归到“平均状态”。我们每个人的生命路径只能经历一次,无法像赌场一样吃群体的长期平均,等着概率在无数次个赌徒中平均化。
为何个体的长期命运大多比“平均值”更差?
在非遍历系统中,个体长期表现往往低于群体平均。这不是偶然,而是系统性的结构特征。光鲜的平均值往往是被极少数创业成功、投资暴富、逆袭上岸的故事拉了上去,更多人的失败从未进入统计。
现实系统在多数情况下是乘法型、且具有路径依赖的特征——比如投资的复利、健康的衰退、声誉的损毁。这类系统的典型特征是:上行有限,下行无底。
一次破产,可能毁掉一生;
一场次错误决策,可能彻底改变命运;
一次失信可能彻底摧毁信任;
而能赚到的财富、涨的绩效、建立的优势却总是有限。
这正是为什么在数学上,乘法型过程的长期增长率并不等于“平均收益”,而是更接近于:
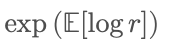
相比之下,群体平均通常用的是算术平均,
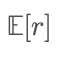
而由于对数函数是严格凹函数,基于Jensen不等式,有:
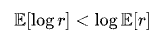
因此,乘法系统的长期增长率(即几何平均)始终小于算术平均。波动越大,这个差距越明显。算术平均是告诉你‘如果永远幸运会怎样’,而几何平均告诉你‘在真实世界里走过风雨之后你剩下多少。
这意味着个体的长期表现总是远低于“群体平均收益”,不是运气不好而是结构使然。
如何做最优决策? 凯利公式的黄金分割线
那么在人生决策中,我们能做点什么避免在长期游戏中归零的命运?如何既不破产出局,还能实现长期复利?
答案是:永远不要 All in,学会凯利下注!
凯利公式(Kelly Criterion)是一种用于重复博弈中的最优下注策略,目标是最大化长期收益的同时避免短期亏光出局。它最初由约翰·凯利(John L. Kelly Jr.)于 1956 年在贝尔实验室提出,原意是解决通信系统中“如何在有噪声的信道中分配信号功率”,以实现信息传输效率最大化。
后来这套理论很快就跨界出圈。
美国数学家、投资奇才爱德华·索普(Edward Thorp)发现凯利公式能够优化财富增长路径。他将凯式带进赌场,在《Beat the Dealer》中首次用它系统性打败了21点庄家,之后又带进了华尔街,在《Beat the Market》中继续“收割”。
这一准则本质上等价于最大化对数期望收益(log-utility),从而兼顾了增长与风险之间的动态平衡。它帮你在“活得长久”和“赚得够多”之间,找到一个最优平衡点。
凯利公式:
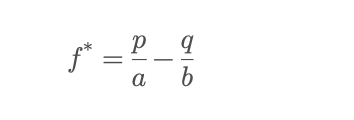
其中,成功的概率是 p,失败的概率是q = 1-p;成功时的收益倍率(不包含本金)是b,失败时的亏损比例是 a(通常是1,如果亏的是全部下注金额)。
回到开篇提到的抛硬币游戏,你可以选择下注一定比例的本金一直玩下去,但每次押多少最合理?

也就是说,凯利公式建议你每次投入总资金的37.5%。押得太多,即使有优势,也可能因为几次连输直接爆仓;押得太少,又错过了本该属于你的增长。
凯利公式的意义就在于:找到那个既能长期赚最多,又能活得下去的点。
补充一点,凯利公式对胜率赔率非常敏感,但现实中这些参数往往不确定或动态变化,因此许多稳健的实践者会选择凯利建议值的一半(被称为半凯利策略)以换取更平滑的收益路径。
模拟实验:10万人翻硬币赌局,多少人能“活”下来?
为了更直观地理解不同的下注策略对个体命运的影响,我模拟了10万个玩家参与开篇的抛硬币游戏,总共进行200轮,每人独立进行游戏。
游戏规则依旧是:本金1000,正面朝上赚80%,反面亏50%。玩家可以选择固定的下注比例:比如押全部(100%),押65%,37.5%,……
结果…… 100%下注的玩家几乎全灭!
最终财富呈“幂律分布”,虽有极少数人暴富,但绝大部分人玩家都破产了。
a. 100%下注:几乎所有人破产
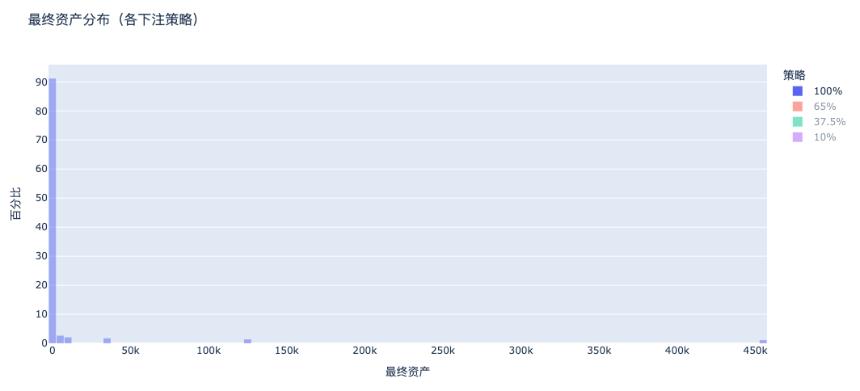
全押策略下的最终资产分布有庞大的左侧贫困峰 + 极细的右侧暴富尾结构:大部分人破产,极少数人赚走所有的钱,这就是博弈不对称性 + 幸存者偏差的真实呈现。
b. 65%下注: 依旧两极分化,仍有大量人破产
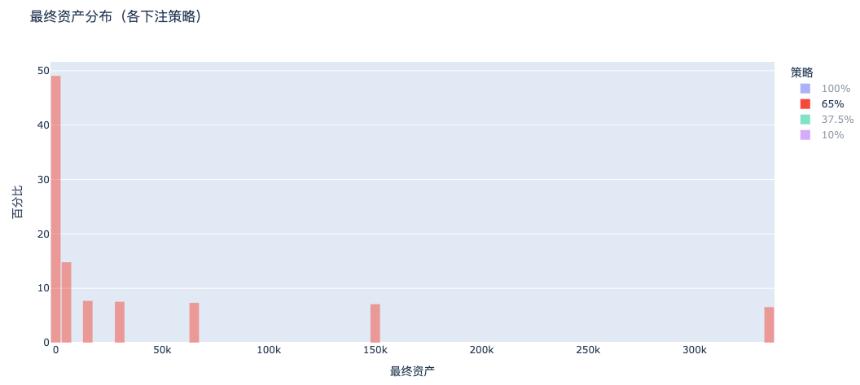
c. 37.5% 下注(凯利公式):财富稳定增长
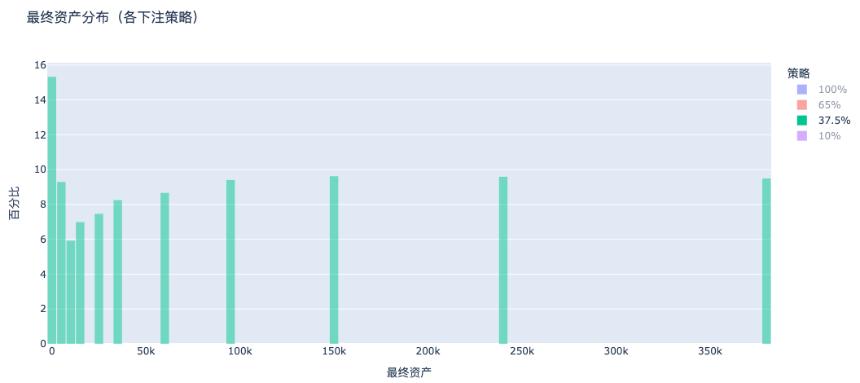
凯利下注策略下,资产分布明显右移,多数人资产增长且分布集中,是最优财富积累模型。
d. 10%下注:几乎无人破产但回报太低
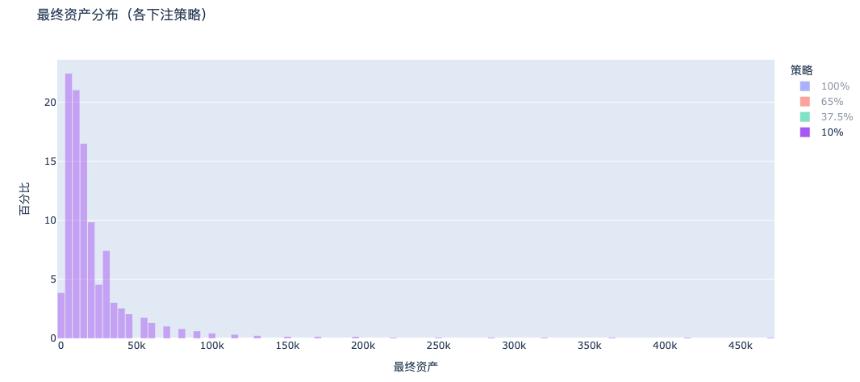
没有了类似全押情况下的破产分布尖峰,但整体财富集中在低资产区。相比之下,37.5% 策略会在右侧拉出明显长尾,实现资产倍增。
凯利下注是唯一兼顾“多数情况下不破产”和“可观增值”的策略,是数学上最优的长期生存策略。这正是凯利公式的精髓:它不是让你赢得最多,而是确保你能活得够久。
凯利公式中的生活哲学
凯利公式告诉我们,长期成功的秘诀是学会把控“下注”的比例。人生不是比谁能打出一次暴击,而是比谁能一直玩下去。
在职业上,不是凭一腔热血裸辞、也不是固守舒适区,是持续布局,提升能力,敢于换道,留一手选择权;
在投资中,是不梭哈暴富,而是根据赔率控制仓位,留得筹码;
在关系里,是不把全部情绪和价值寄托于一人,而是投入同时保有自我;
在成长和自律上,不靠一次爆发去获得改变,而是通过稳定、复利式地优化生活结构。
人生就像一场漫长的游戏,你的目标不是赢一次,而是确保自己能一直玩下去。只要不出局,一定会有好事发生。
- 1美联储2025年降息对非必需消费品与科技股的深远影响
- 2币安人生上线币安Alpha,三天市值突破1.5亿美元的背后
- 3比特币引领加密货币市场:4.35万亿美元市值背后的战略配置与宏观经济驱动
- 4比特币今日新闻:飙升至历史高点,对冲美元贬值与政策波动成焦点
- 5「币安人生」暴涨背后的流量密码:CZ与何一的推波助澜
- 6OpenAI将ChatGPT重塑为多功能应用平台,推出App SDK与AgentKit
- 7Aster空投计划:打击洗盘交易与市场抛售压力的博弈
- 8Berachain/比特币市场分析(2025-10-05):短期支撑位或成关键
- 9美国通过GENIUS法案:稳定币监管新时代巩固美元数字主导地位
- 交易所
- 币种
| 排名 | 交易所 | 成交额 |
|---|---|---|
| 1 |  币安网 币安网 |
¥1.21万亿 |
| 2 |  欧易OKX 欧易OKX |
¥3,983.14亿 |
| 3 |  HTX HTX |
¥598.55亿 |
| 4 |  Coinbase Coinbase |
¥225.56亿 |
| 5 |  大门 大门 |
¥2,806.61亿 |
| 6 |  Bitget Bitget |
¥2,539.58亿 |
| 7 |  Bybit Bybit |
¥3,130.00亿 |
| 8 |  双子星(Gemini) 双子星(Gemini) |
¥12.50亿 |
| 9 |  Upbit Upbit |
¥176.04亿 |
| 10 |  Crypto.com Crypto.com |
¥771.42亿 |

 泰达币
泰达币 以太坊
以太坊 比特币
比特币 USD Coin
USD Coin Solana
Solana 币安币
币安币 瑞波币
瑞波币 First Digital USD
First Digital USD 狗狗币
狗狗币 Sui
Sui